[algorithm] 동적 계획법

DP 사용 조건

1. 최적 부분 구조
   • 큰 문제를 작은 문제로 나눌 수 있으며 작은 문제의 답을 모아 큰 문제를 해결(보통 점화식을 세운다)
2. 중복되는 부분문제
   • 동일한 작은 문제를 반복적으로 해결

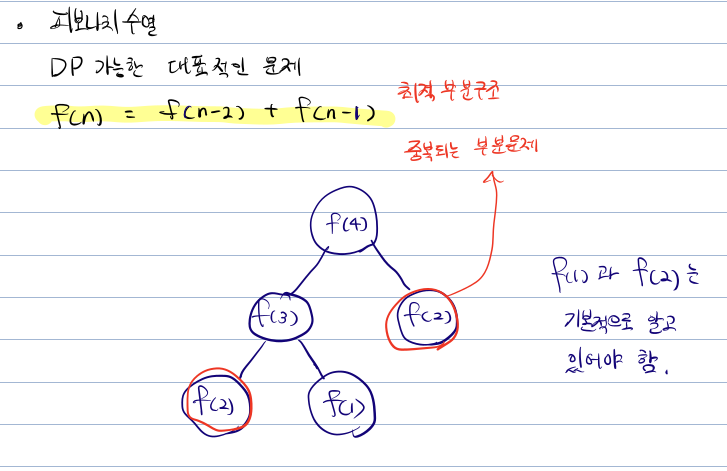
풀이 방식 두 가지

DP를 구현한 소스코드들은 bottom-up, top-down process로 나눌 수 있다. bottom-up은 귀류적인 느낌, top-down은 연역적인 느낌이 든다.

top-down 방식(재귀)

중복되는 부분문제를 해결하기 위해 메모이제이션을 이용한다. 계산결과를 메모해뒀다가 같은 문제를 호출했을 때 그 결과를 그대로 가져오는 방법이다. 보통 dp, d, cache라는 이름으로 배열을 선언하여 그곳에 기록한다.

bottom-up 방식(반복문)

가장 전형적인 DP풀이이다. 가령 위의 피보나치의 경우

for(int i = 3; i < n; ++i)
	cache[i] = cache[i - 1] + cache[i - 2];

분할 정복과의 차이점

둘 다 최적부분 구조인 문제에서 사용가능하나 중복되는 부분문제가 존재한다는 점에서 차이가 있다. 퀵정렬의 경우, 기준 원소인 피벗이 한 번 정해지면 그 피벗의 위치는 더이상 변하지 않는다, 즉 중복되는 경우가 없으므로 DP를 사용하지 않는다.

접근 방법

1. 다이나믹 프로그래밍의 조건인지 판단
2. 점화식을 세움
3. for문으로 cache를 0부터 채워나가거나 재귀호출을 통한 완전탐색을 구현한 뒤 메모이제이션을 넣음

끝