[MATH/공수] 고계 선형상미분방정식 푸는 법

고계 선형상미분방정식

이전 포스팅에서 2계 선형상미분방정식 푸는 법을 설명했는데 고계도 이와 비슷하다.
제차의 경우 기본개념은 2계와 마찬가지로 1계 미방들의 system equation으로 바꾸어서 행렬로 표현한 다음에 고윳값을 구해 기저들의 선형결합으로 표현하는 것이고,
비제차의 경우 2계와 똑같이 제차의 일반해와 비제차의 특수해를 선형결합으로 표현하는 게 기본이다.
결국 풀이법은 앞선 포스팅과 같다.

제차 선형상미분방정식

일단 선형이니까 기저들의 선형결합으로 일반해를 표현할 수 있다.
여기서, 우리가 구한 해들이 기저인지 아닌지 어떻게 아느냐가 문제인데, 앞선 포스팅들에서는 그냥 특성방정식이나 보조방정식 구하고 이거 1차독립 맞아요하고 넘어갔지만 여기서 한번 다루어보자. 여기서 증명이 되면 2계도 마찬가지로 증명이 된다.
기저임이 증명되려면 그것들 각각이 모두 linearly independent해야 한다. 기저들을 한데 모아 하나의 matrix로 만들어 보자.

타자치기가 상당히 귀찮아서 말만적고 넘기고 싶지만 미래의 나를 위해 이미지라도 올려보자면

기저를 변환시키는 행렬의 determinant는 기저 변환 이후에 단위 공간이 어느 비율로 변화되었는가를 의미한다. 이게 이해가 되지 않으면 Essence of linear algebra의 6강까지 보고 오면 된다.

그래서 저 위의 matrix의 det를 구했을 때 0이 나온다면 그건 공간자체가 한차원 다운되었다는 걸 의미하고 이는 기저라고 생각되는 벡터의 개수만큼의 차원이 안나온다, 즉 특정 벡터가 중복되었다는 것이다. 그러므로 이 경우 1차 종속이다. 그리고 위와 같은 matrix의 determinant를 Wronskian이라고 한다. Wronskian이 0이면 1차 종속이고 기저가 아니라는 것이다. 반대로 0이 아니라면 기저가 맞다.
앞으로의 내용에서 우리가 구한 기저들의 Wronskian을 계산하여 그게 기저가 맞다는걸 증명해 보자.

상수계수를 갖는 제차 선형상미분방정식

앞선 포스팅에서

즉, 선형상미분방정식의 해는 기저들의 linear combination으로 나타낼 수 있다는 것이고 이는 고차 선형미분방정식의 풀이의 핵심이다. 미리 설명하면, 고차 항들 각각을 독립적으로 한번만 미분한 변수로 생각하고 그것들로 1차 선형미분방정식들의 선형연립방정식을 세운다. 그 연립방정식을 행렬곱으로 표현하고 거기서 나온 기저해들의 linear combination이 고차 미분방정식의 해 space(일반해)가 된다는 것이다. 여기서 나온 기저해들은 지수에 행렬을 달고 있는데 이러면 불편하니까 기저변환행렬에 해당하는 행렬의 고윳값을 구해서 행렬을 상수로 바꿔버린다. 그말은 곧 고차 미방을 풀려면 1차 선형미방의 해를 구할 줄 알아야 한다는 것이다.

라는 문단을 다시 가져와 보자.

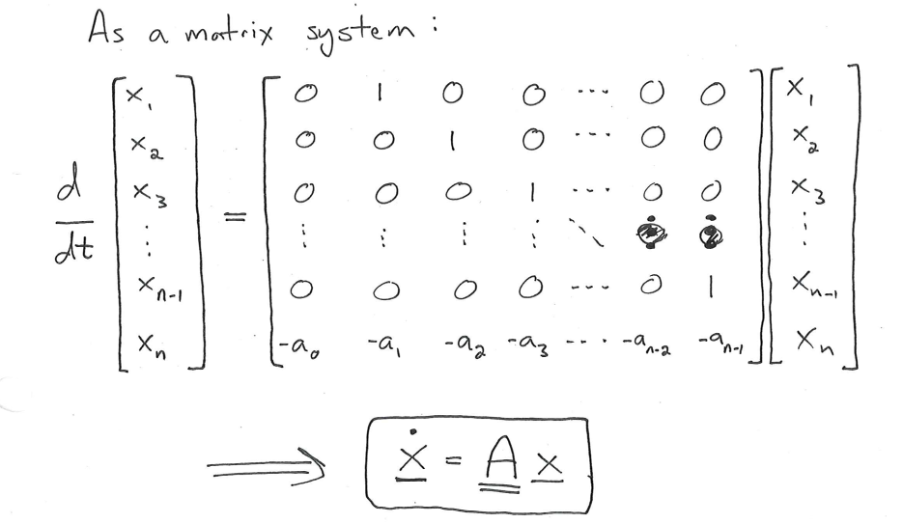
고윳값을 구하는 식은 \(y = e^{\lambda x}\) 를 때려넣어서 나온 방정식인 characteristic equation과 같다(제차인 경우에만 풀린다).

characteristic equation을 풀었을 때,

1. 서로 다른 실근
2. 단순 복소근
3. 다중 실근
4. 다중 복소근

이 네 가지의 경우가 발생한다.
Wronskian을 구해보면 \((-1)^\frac{n(n-1)}{2}V\) 이 나오고, 여기서 V는 람다들의 차의 곱이다. 그래서 저 행렬식이 0이 나오지 않으려면 람다들의 차가 0이 되면 안되고 특성방정식의 모든 근이 서로 달라야 기저가 된다는 결론이 나온다. 그래서 3번이나 4번처럼 다중 실근이나 복소근이 나오는 경우, 해당 기저를 바탕으로 일차독립인 새로운 기저를 만들어낸다. 2계에서 했던 것과 마찬가지로 x의 거듭제곱을 안겹칠때까지 곱하면 된다.

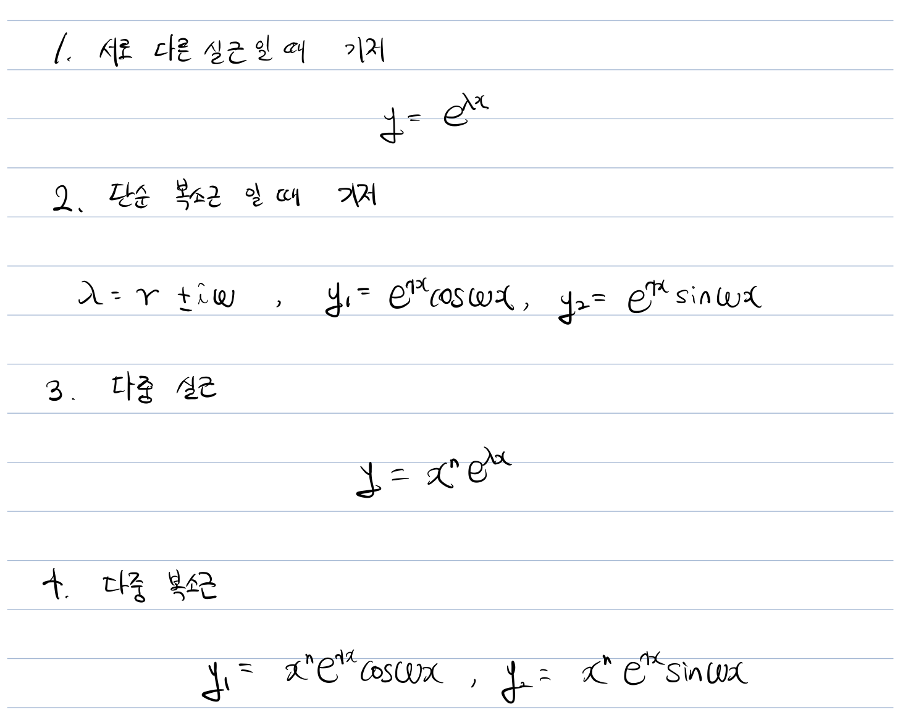
n계 Euler-Cauchy Eq

이전에 2계에서 했듯이 \(y = x^n\) 을 기저라고 해서 때려넣고 보조방정식 세워서 구하면 된다.

비제차 선형상미분방정식

기본적인 개념은 2계에서 소개했던 방식과 같다.
특수해를 어떻게 구하느냐가 문제인데, 2계와 마찬가지로 미정계수법, 매개변수변환법이 있다.

미정계수법

때려맞추는 건데 규칙은 있다. 규칙도 2계랑 똑같다.

여기서 해당하는거 때려넣으면 된다.

매개변수변환법

2계에서 임이의 계수 n으로 확장하면 된다.

\[y_p(x) = \sum_{k=1}^{n}y_k(x)\int\frac{W_k(x)}{W(x)}r(x)dx\]

이것도 마음같아서는 증명하고 싶은데 유튜브에도 관련 영상이 몇 없는 것 같아 그냥 외우련다.
아, Wronskian에 k라는 첨자붙은게 뭔가싶을 텐데 k번째 열을 마지막 요소만 1인 zero column vector로 치환한 것이다.

끝